第1章[pdf]:
1.1 简介
1.2 先进飞翼设计 - 周期2
1.3 集成飞机设计和多学科优化MDO
1.4 空气动力学设计和计算空气动力学CFD
问题复习:
- 解释为什么图1.14 (附在下方以便参考)的亚音速平面布局升阻比L/D曲线会随着马赫数的增加而下降。
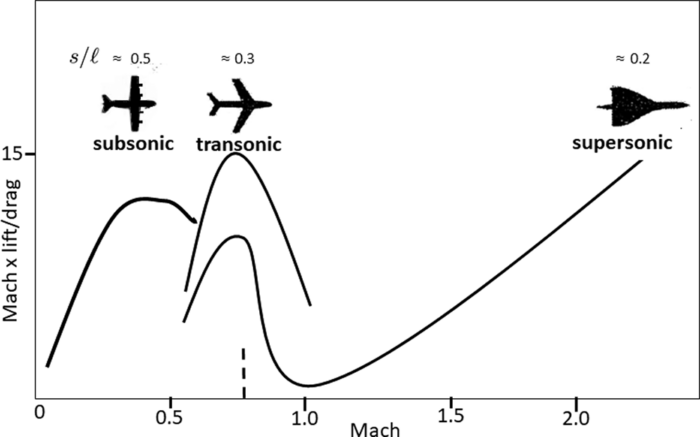
- 解释/阐述弱耦合多学科优化(MDO)的概念。
- 提供并解释CFD数据和其他学科交换的例子。
- 图1.3(附在下方以便参考) 显示了最大升阻比 L/D max 随着展弦比AR 的变化。 使用近似关系 Eq. 1.5 检查曲线的形状。
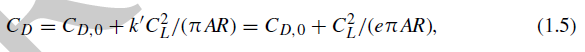
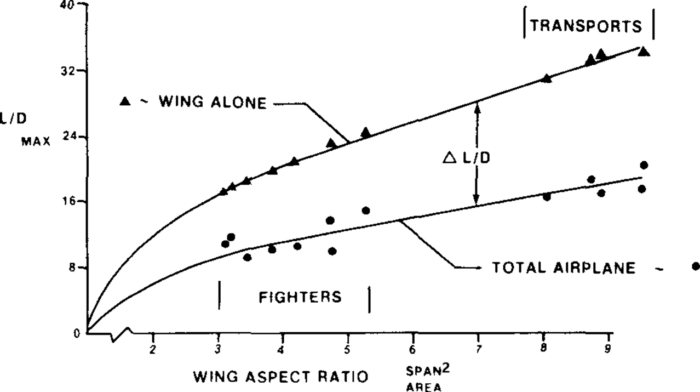
- 下列有限维优化任务,
min g(y), y = (flow) variable dim N
s.t. f(x,y) = 0, x = shape parameters of dim M, M << N
为什么伴随法计算梯度 dg/dx 的计算成本是使用直接梯度法计算成本的 1/M ?
提示: dg/dx = dg/dy dy/dx; df/dx + df/dy dy/dx = 0, 所以直接梯度:
dy/dx = – (df/dy)-1 df/dx
df/dy 是 NxN 矩阵, dy/dx 和 df/dx 是 NxM 矩阵,dg/dy 是 1 x N 向量。
则,
dg/dx = – dg/dy (df/dy)-1 dy/dx.
这个矩阵的乘积该如何计算?
- 这是一架 Piper J-3 Cub 飞机和海平面大气条件的相关数据:
b = 10.74 m, MTOW = 550 kg, S = 16.6 m2, ρair = 1.2 kg/m3.
最佳爬升速率 (Vy) 450 ft./min, 据对高度限制为 14,000 ft., 巡航速度 73 mph,
最高速度 83 mph, 失速速度 (Vs) 39 mph, 最佳滑行速度 (Vgl) 50 mph。
Piper飞机的阻力极曲线图可能可以得到,但我们可以使用上述数据来进行近似计算:
CD = CD0 + k CL2
运用上述近似计算公式可以得到相当不错的估算结果;因此,需要得到 k 和 CD0 的数值。首先,升力线理论给出了 k 的估算值,
k = 1/(e π AR)
其中 e 是展弦比效率银子,其最大值为1,我们将其取为0.85。
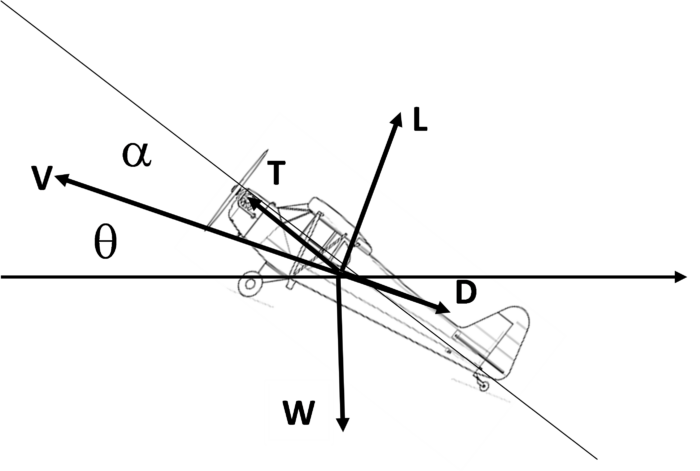
在考虑攻角 α 和飞行轨迹角度 q 的情况下,假设推力矢量与飞机水线对齐的平衡方程为:
T sin α + L – W cos α = 0 (1)
T cos α – D – W sin α = 0 (2)
在滑行中,推力 T = 0。根据方程(1) 和 (2) 的比率,可以得出最佳滑行角度为:that the best glide angle has
θopt = – atan(1/max(CL(α)/CD(α)) = – atan(sqrt(k CD0)) approx = – sqrt(k CD0)
CDopt = 2 CD0
使用上述结论在方程 (2) 中推导得出的结果是:
CD0 = [W sqrt(k) / (ρair S Vgl2)]2
生成的这些数值已经在cfd.m 函数中的表格里使用,用于后续的练习和计算中。
- W 和 S 应被视为设计参数。对于平直水平飞行的飞机,当 θ = 0 时,有四个变量: T/W, W/S, α 和 V,并符合下列两个约束关系:
T/W W/S cos α -1/2 ρair V2 CD(α) = 0
T/W W/S sin α + 1/2 ρair V2 CL(α) – W/S = 0
该经典情况通过地毯图阐明。将 W/S 重命名为 x, 将 T/W 重命名为 y:
x y cos α -1/2 ρair V2 CD(α) = 0
x y sin α + 1/2 ρair V2 CL(α) – x = 0
绘制一个用于海平线飞行的T/W (y) -W/S (x) 图表,如下所示:
% make lists Vlist(1:nV) and alist(1:na)for i = 1:nV
for j = 1:na
% solve equations for x and y to get x(i,j) and y(i,j)
end j
% plot the curve {x(i,:),y(i,:)}
end i
for j = 1:na
% plot the curve {x(:,j),y(:,j)}
end j
图表显示:对于给定的推力和重量,可以以两种不同的 (α, V) 飞行,一种是大攻角α 低速 V, 另一种是小攻角α 高速 V。这两者在维持飞行的最低推力处重合。假设你正在以最佳巡航速度飞行,如果增大攻角 α 会发生什么?在不改变攻角 α 的情况下,加大油门会怎样?
- 文件夹 .../Ch1 包含使用 Octave 优化工具箱
optim中的fmincon优化器运行非线性优化问题的例程。fmincon通过求解一个由目标函数objf(X)、参数 X 的上下边界 lb 和 ub 以及由函数 constr(X) 定义的非线性(等式或不等式)约束的非线性优化问题来实现优化。运行脚本opt1.m来进行优化; 通过将全局变量 DEMO 设置为 1 或 2 来选择问题。
DEMO = 1 研究在海平面高度平直水平 (θ = 0) 飞行中寻找最小推力所需的攻角 α 和空速 V 的问题 – 即最佳巡航问题。
min over (α,V) T = D/cos α= q S CD/cos α
q = 1/2 ρair V2
subject to the constraint
L = q S CL >= W, - T sin α = W - q S CD tan α .
由于 W = MTOW g、 S、和 ρair 是常数, 我们可以将问题进行尺度变换。
设 r = 1/2 S ρair, w0 = W/r;
寻找最值优化问题:
min V2 CD(α)/cos α over X = (α,V) subject to the constraint V2 CL(α) >= w0 - V2 CD(α) tan α
空气动力学由 CL(α)、 CD(α) 表格定义,因为 cfd 函数只需要在这些表格中进行插值,并返回 [CL CD] 的值。
函数 objf 调用 cfd 获取性能参数 prop, 并返回 FoM。约束函数 constr 调用 cfd 获取参数 prop 并返回 c 值,且值必须 <= 0。
演示程序 opt1.m 解决了这个问题:
- 运行程序,使用不同的机翼面积(不同的机翼载荷),并记录最佳的 α 。
- 通过分析,验证最优点出现在可将CL/CD + tan α 最大化的 α 处这个结论 – 请确定这些项中哪些项占主导地位?
- 然后展示,最大升阻比 L/D max 的点可通过原点直线与阻力极曲线的切点找到。
- 将你得出的结果和练习6中给出的巡航速度相比较。
接下来的任务是修改 objf 和 constr 两个函数,当推力 T 为最大推力 Tmax 时,求解 α、V 、θ、T 使得爬升速率 V sin θ 达到最大爬升速率。设 r = 1/2 S ρair, w0 = W/r。
max V sin θ over (α,V,θ,T)
T cos α – V2 CD(α) – w0 sin θ = 0
T sin α + V2 CL(α) – w0 cos θ = 0
T <= Tmax/r
通过在opt1 中将全局变量设置为 DEMO = 2 来解决该问题,此时 constr定义了两个等式约束,T的限制为在 ub 中定义的上限。你的任务是填写缺失的代码行,并使用不同的初始值进行优化。